摘要：很多教学辅导书中有一道光学例题，其解法有错误。为了澄清此错误，避免再以讹传讹，今对其错误进行剖析，并应用Excel进行探究，利用几何画板制作的课件进行动态演示。
关键词：错解原因分析；正确解法；问题探究；动态演示
很多教学辅导书中有这样的一道光学例题：
题目：某三棱镜的横截面是一直角三角形，如图1所示，∠A=90o，∠B=30o，∠C=60o，棱镜折射率为n，底面BC涂黑，入射光沿平行于底面BC的方向射向AB面，经AB面和AC面折射后射出。
（1）求出射光线与入射光线之间的夹角δ。
（2）为使上述入射光线能从AC面上射出，折射率n的最大值。
 |
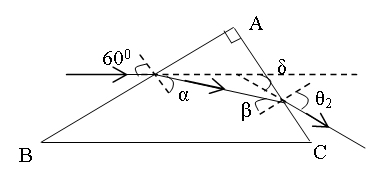图 1 |
[原解] （1）设光在AB面上的折射角为α，在AC面上的入射角为β，折射角为θ2。
 |
一、错解原因分析与正确解法
此题第（1）问解答是正确的，而第（2）问解答是错误的。要使光线能从AC面射出，为什么要应有θ2≤60o，理由何在？实际上，由于折射率不同，在AB面的折射角α就不同，就会使得在AC面上的入射角也不同，要使得光线能从AC面上射出，入射角β不得大于其临界C。即
 |
由①④两式得
 |
上述θ2≤60o的错误得出，笔者猜测可能是通过此式，利用α和β一些特殊的角度，如当α =
30o时，β = 60o，此式不成立；当α = 45o时，β = 45o，此式成立，从而得出α≥β，则θ2≤60o，显然是片面的、错误的。
由②⑤两式可进一步得到
 |
即α＞40.8933946o
可见，只要满足α＞40.8933946o,就有光线从AC面出射，而在此范围内，也有β角大于α角的时候，如α角为42o时β角为480，θ2就大于60o，所以，此例题的第二问解答是错误的。
正确的解答应是：
 |
 |
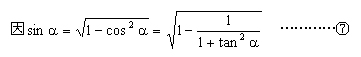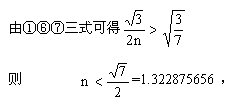或由③式 
，亦可得出此结论。
可见，折射率是一个比
小的值，其值到底是多少很能精确确定，故折射率是没有最大值的。因此，笔者认为此题第（2）问应改成“为使上述光线能从AC面上射出，折射率n应满足的条件。”这样会更好一些。
二、问题探究
为了进一步得出光线能从AC面上射出，折射率应满足的条件，可用Excel来进行探究。
1．建立工作表
启动Excel软件，新建一个xls文件。在表1所示的A1、B1、C1、D1、E1、F1、G1单元格中分别输入θ1、α、β、sinα、sinβ、n、θ2。在A2中输入60，然后自动填充至A32，在B2、B3中输入30、31，选中B2、B3单元格，然后自动填充至B32。
 |
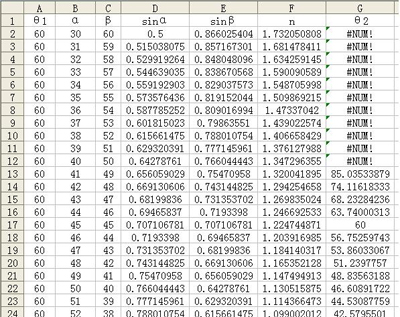表 1 （点击图表放大） |
2．输入函数公式
在单元格C2中输入“=90－A2”、D2中输入“=sin(B2*PI()/180)”、E2中输入“=sin(C2*PI()/180)”、F2中输入
“=sin(A1*PI()/180)/D2”、G2中输入“=ASIN(F2*E2) *180/PI()”,选定C2、D2、E2、F2、G2单元格，向下拖动自动填充柄至G32，便自动计算出相应的各个量的值，如表1所示。
3．条件的得出
从表1中可以很清楚地得出：在α角为30o～40o的范围内，在θ2～θ12单元格中出现“#NUM！”的错误提示，说明了sinθ2的值大于1。在α≥41o时，θ2均有解，有大于60o，也有小于或等于60o。在40o至41o之间插入一行，再在B13中输入40.8933947（因α＞40.8933946o），然后回车，便可得出此时的折射率为1.322875654，接近1.322875656，从AC面上出射光线的折射角为89.99656792，如表2所示，因此，为使光线能从AC面上出射，棱镜的折射率必须小于
，而不是最大值为
。其数据源见“对一道光学例题的探究.xls”。
 |
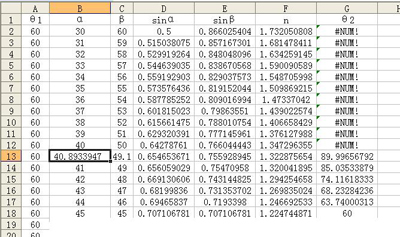表 2 （点击图表放大） |
三、动态演示
|
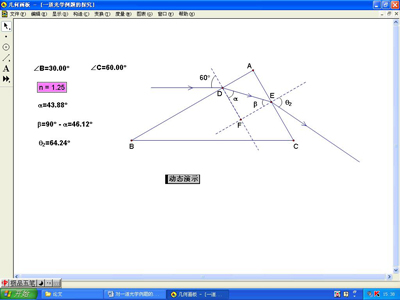图 2 （点击图表放大） |
利用“几何画板”软件制作一个动态演示课件（制作过程略），单击“动态演示”按钮（或选中折射率参数n，按键盘上的“＋”或“－”增大或减少参数n），随着折射率参数n的变化，经AB面的折射角α和AC面的入射角β与折射角θ2都发生动态变化，光线的传播方向也随之发生动态变化，如图2所示。当折射率n的数值超过1.32时，在AC面就没有光线射出，由此可得：为使光线能从AC面上出射，棱镜的折射率必须小于。其动态演示课件见“一道光学例题的探究.gsp”。